ElGamal是个啥子玩意

很早之前就听说ElGamal加密算法是一种公钥密码，但是具体实现和用途不甚了解，今天阅读了 A PUBLIC KEY CRYPTOSYSTEM AND A SIGNATURE SCHEME BASED ON DISCRETE LOGARITHMS 一文，故去了解了一下。特开此文，记录一下

省流：ElGamal是DH密钥交换的抵抗中间人攻击版本

---

ElGamal加密算法是一个基于DH密钥交换的非对称算法，可以定义在任何循环群上，它的安全性取决于循环群上的离散对数难题

离散对数问题指的是：

• 已知 $a,b,n$ ，计算$ a^b\mod n$ 是简单的。
• 已知 $a,(a^b\mod n),n$ ，计算 $b$ 是困难的。

Diffie-Hellman 密钥交换过程：

1. Alice 和 Bob选定一个素数 $p$ ，以及它的一个原根 $g$
2. Alice 选择一个密钥 $a$ ，计算 $A=g^a\mod p$ ，发给 Bob
3. Bob 选择一个密钥 bb ，计算 $B=g^b\mod p$ ，发给 Alice
4. Alice 计算 $s=B^a\mod p$ ，Bob 计算 $s=A^b\mod p$
   这样，Alice 和 Bob 就共享了一个密钥 $s=g^{ab}\mod p$

通俗理解：在调色板上将两种颜色混合容易，而将两种颜色分开是困难的。

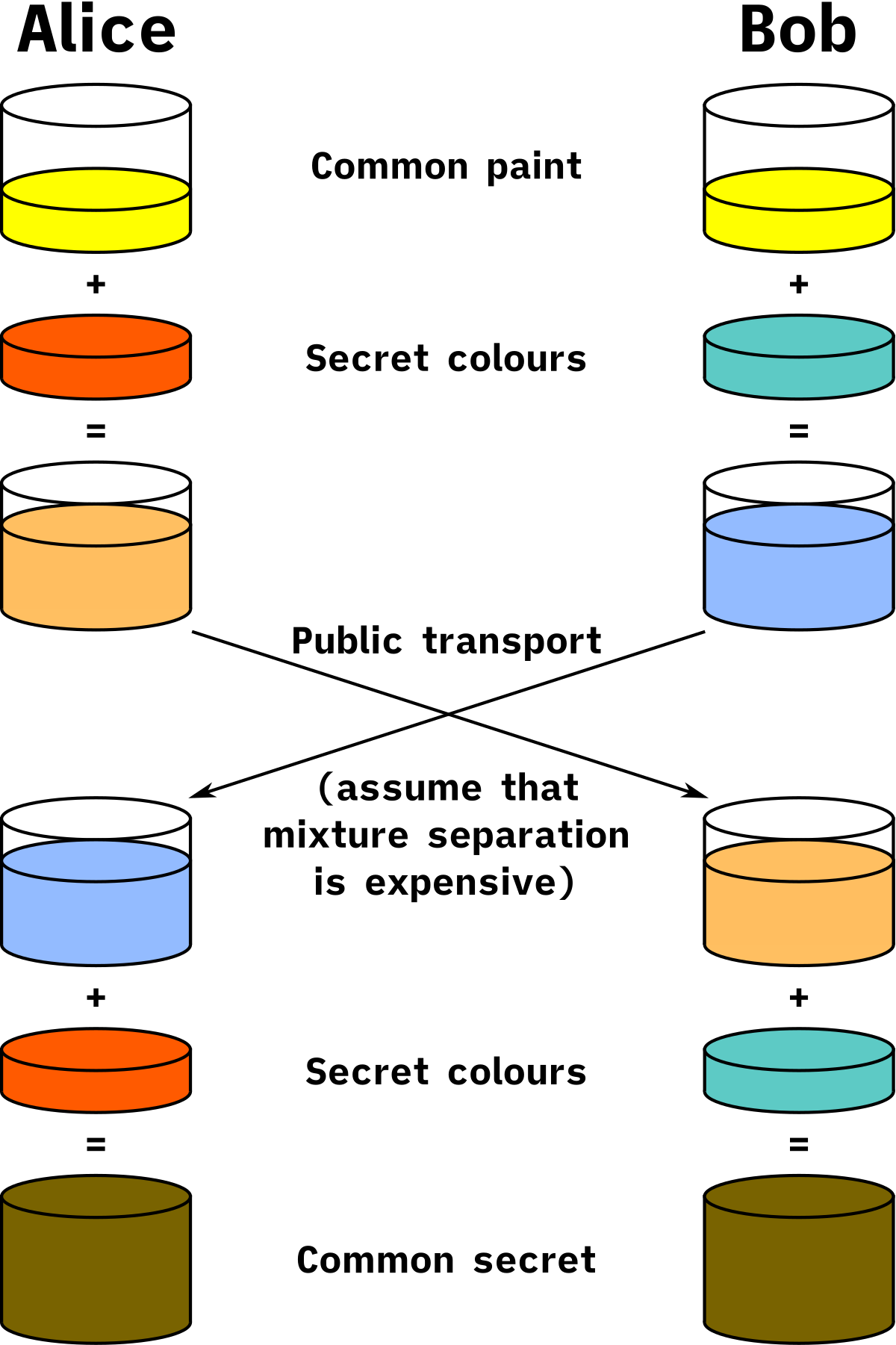
由于离散对数问题是一个数学困难问题，在选择了合适的 $p$ 和 $g$ 时，Diffie-Hellman 密钥交换协议被认为是 $\textcolor{red}{窃听安全}$ 的。攻击者 Eve 在已知 $p, g, (g^a\mod p), (g^b\mod p)$ 的情况下，难以计算出 $s=g^{ab}\mod p$

$\textcolor{red}{缺陷:无法抵抗中间人攻击}$

DH 本身没有提供任何身份认证，因此容易遭受中间人攻击：

• 中间人 Eve 假装自己是 Bob 与 Alice 通信 $s_1=g^{ac}\mod p$
• 中间人 Eve 假装自己是 Alice 与 Bob 通信 $s_2=g^{bc}\mod p$
• Eve 将 Alice 发来的消息用 $s_1$ 解密，使用 $s_2$ 加密，发送给 Bob
• Eve 将 Bob 发来的消息用 $s_2$ 解密，使用 $s_1$ 加密，发送给 Alice
• Alice 和 Bob 对此一无所知，还无知地以为在与对方通信

需要一种能验证通信双方身份的机制 (如签名) 来防止这类攻击

---

ElGamal 加密算法：

本质上就是用 DH 获得一个密钥，然后用它加解密消息。

密钥生成：

1. Alice 和 Bob 选定一个素数 $p$ ，以及它的一个原根 $g$
2. Alice 选择一个私钥 $X_A$ ，计算公钥 $Y_A=g^{X_A}\mod p$，公开
3. Bob 选择一个私钥 $X_B$ ，计算公钥 $Y_B=g^{X_B}\mod p$ ，公开

假如 Bob 要给 Alice 发送一条消息 $m$ ，加密过程：

1. Bob 计算密钥 $k=(Y_A)^{XB}\mod p=g^{X_AX_B}\mod p$
2. Bob 发送 $c_1=Y_B, c_2=k\cdot m\mod p$

Alice 收到密文，解密过程：

1. Alice 计算密钥 $k=(c_1)^{X_A}\mod p=(Y_B)^{X_A}\mod p=g^{X_AY_A}\mod p$
2. Alice 解密消息 $m=(c_2\cdot k^{−1})\mod p$

实现代码：

from Crypto.Util.number import *

p = None ; g = None
pub = None#公钥也是公共可见的
c = None#加密方加密后并传输给解密方的密文，这个也是可以被攻击者截获的

#初始化，公共可见的大素数和生成元
def init():
    global p , g
    p = getPrime(512)
    g = 2

#接收方(A)需要干的事情，即生成密钥（包括公钥和私钥
def reciver_need_do():
    global pub
    a_pri = bytes_to_long(b'I am priviate key of A.')
    a_pub = pow( g , a_pri , p )
    pub = a_pub
    return a_pri

#发送方(B)需要进行的加密操作，生成密文并
def ElGamal_encode():
    m = bytes_to_long(b'miao miao miao wo shi ming wen 233')
    k = getRandomInteger(10)
    c1 = pow( g , k , p )
    c2 = m * pow( pub , k , p ) % p
    return c1 , c2

#解密方需要进行的解密操作
def ElGamal_decode( pri ):
    global c
    c1 , c2 = c
    c1 = pow( c1 , p-2 , p )
    m = c2 * pow( c1 , pri , p ) % p
    return m

if __name__ == '__main__':
    init()
    a_pri = reciver_need_do()#返回接受者的私钥，a_pri只有接受者可以用
    c = ElGamal_encode()#B将信息进行加密，然后传给A
    m = ElGamal_decode( a_pri )#A使用自己的密钥，对信息进行解密
    print( long_to_bytes(m) )