阅读《Identity-Based Chameleon Hashing and Signatures Without Key Exposure》一文时，遇到了Decision Diffie-Hellman Problem (DDHP)这一概念，头一次遇到，便搜索了一下，打算学习学习；没想到捅了老挝——一个DH密钥交换算法能衍生出各式各样的东东

没办法了，学吧

由于种种原因（我比较懒），目前只学DDHP，其他的先挖个坑

DDHP

论文里的描述

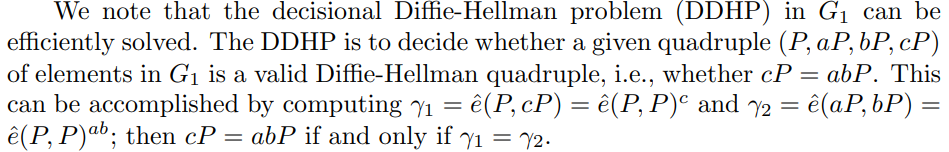
大致内容：在特定的群 $G_1$ 中，可以通过计算双线性映射的方式有效地判断一个四元组是否满足Diffie-Hellman条件

区别 DH DDHP
目的 用于密钥交换，建立安全通信 判断给定值是否符合Diffie-Hellman关系
功能 生成共享密钥 验证一个数值是否是由特定的私钥生成的
安全性基础 基于离散对数的困难性，安全性与密钥长度和生成元选择有关 直接依赖于离散对数问题的安全性，特别是在无法计算 $g^{ab}$ 的情况下

代码展示

（有点草率，但是感觉思想很到位）

1
2
3
4
5
6
7
8
9
10
11
12
# 假设我们已经有 A、B 和一个待验证的 C
C = pow(g, a * b, p)  # 假设这是我们计算出来的 C

# 验证DDHP
def verify_ddhp(p, g, A, B, C):
    # 计算 g^(ab) mod p
    calculated_C = (pow(A, b, p))  # K = A^b mod p
    return calculated_C == C

# 输出验证结果
is_valid = verify_ddhp(p, g, A, B, C)
print(f"Is C valid? {is_valid}")

结合双线性映射

问题描述

给定四个元素$(P,aP,bP,cP)$，其中：

$P$ 是群中的生成元

$aP$ 和 $bP$ 是两个通过标量乘法得到的公钥

$cP$ 是待验证的值

DDHP的目标是判断 $cP=abP$ 是否成立

解决步骤

  1. 计算双线性映射

  1. 判断条件

    若$\gamma_1=\gamma_2$，则可以确认 $cP$ 是有效的Diffie-Hellman四元组，即 $cP = abP$