记录概率论的学习内容

目录

一、随机事件和概率

1.古典概型

2.几何概型

3.重要公式

4.独立性判定

二、一维随机变量及其分布

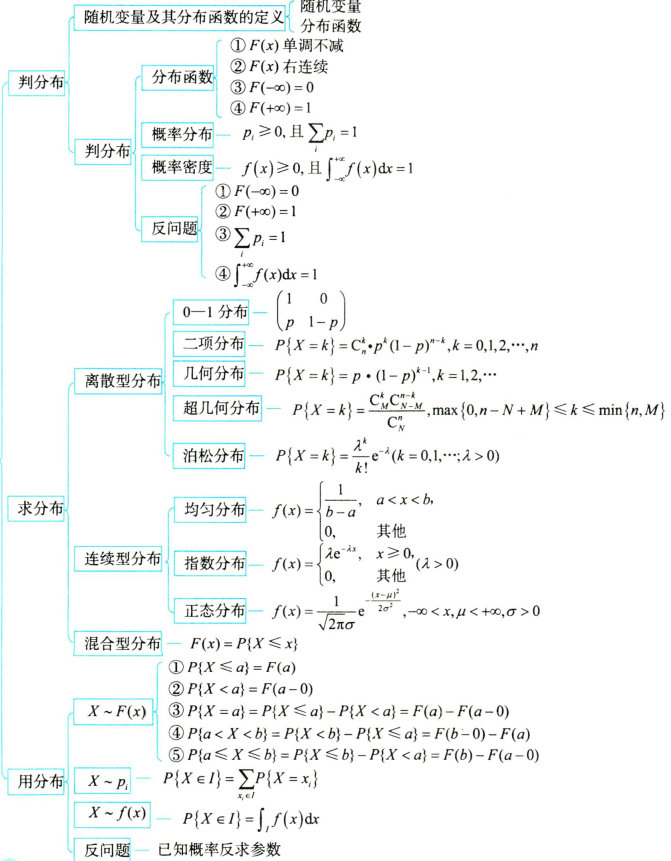
1.判分布

随机变量：$X:\Omega\rightarrow\mathbb{R}$

分布函数：$X\sim F(x),F(x)=P(X\leq x),F(x)\in[0,1]$

对于连续型$F(x)=\int_{-\infty}^{x}f(t)dt,x\in\mathbb{R}$

A

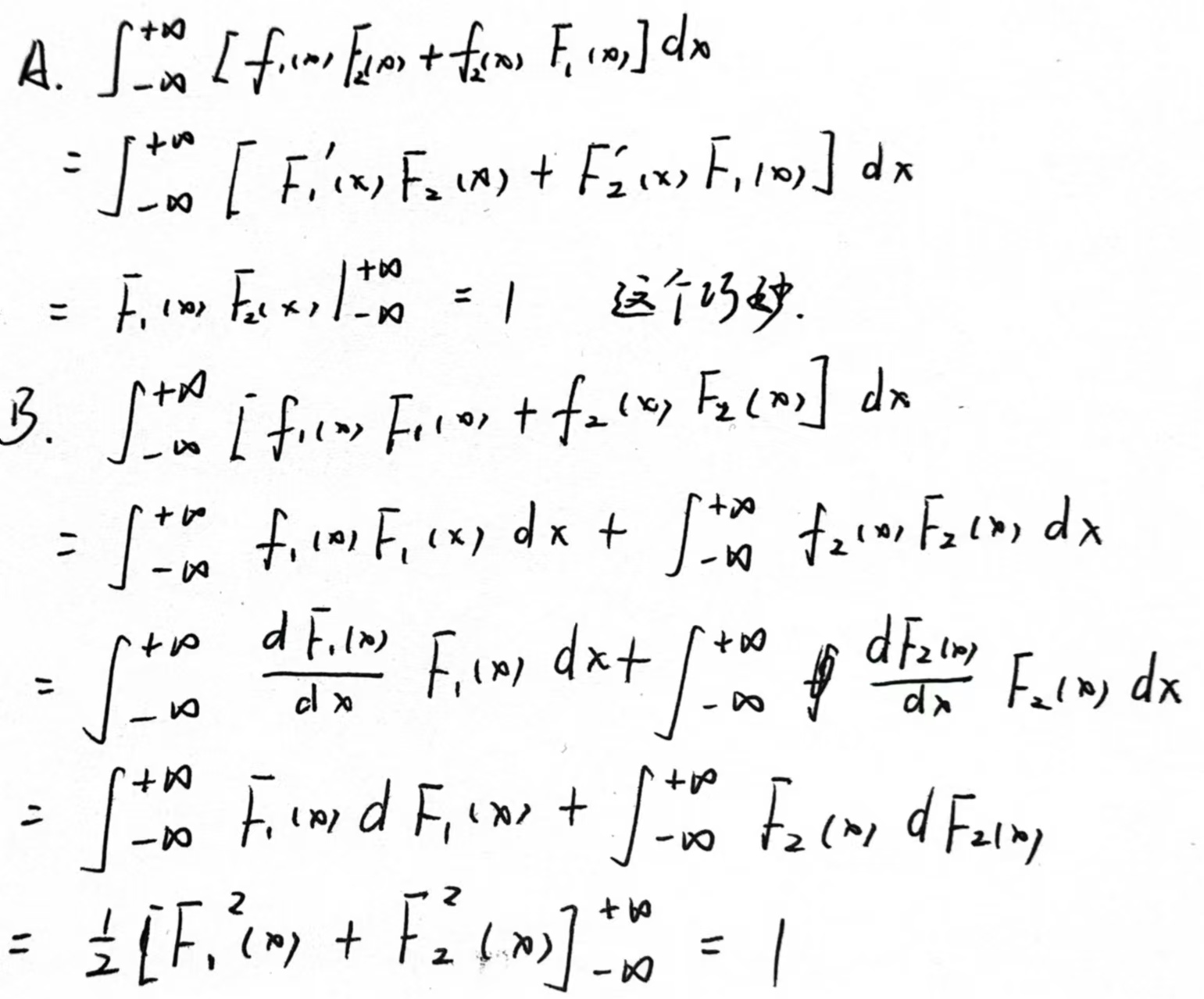
B选项解法二：也可以使用部分积分公式$\int udv=uv-\int vdu$

部分积分公式推导过程

其中：$u=v=F(x)$

带入部分积分公式：$\int F(x) dF(x)=[F(x)F(x)]|_{-\infty}^{+\infty}−\int F(x)dF(x)$

故 $\int F(x) dF(x)=\frac{1}{2}$

则 $g_2(x)$ 可以作为概率密度

$g_1(x),g_2(x),g_3(x)$可以作为概率密度， $g_4(x)$ 不能作为概率密度

C

2.求分布

  • 离散型分布

    • 0-1分布 $X\sim B(1,p),X(伯努利计数变量)\sim \left(\begin{array}{l}0&\quad1\p&1-p\end{array}\right)$

    • 二项分布 $X\sim B(n,p)$ 分布律 $U_k=P{X=k}=C_n^kp^k(1-p)^{n-k}$

    • 几何分布 $X\sim G(p)$ 首中即停止 $P{X=k}=p\cdot (1-p)^{k-1}$

      无记忆性

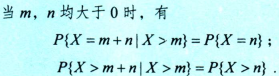
    • 超几何分布

    • 柏松分布 稀有事件的概率 $P{X=k}=\frac{\lambda^k}{k!}e^{-\lambda}$，$EX=\lambda$

泊松定理 若$X\sim B(n,p)$，当$n$很大，$p$很小，$\lambda=np$ 适中时，二项分布可用泊松分布近似表示；一般地，当$n>20,p<0.05$ 时，用泊松近似公式通近二项分布效果比较好，特别当$n>100,np<10$ 时，逼近效果更佳

B

8

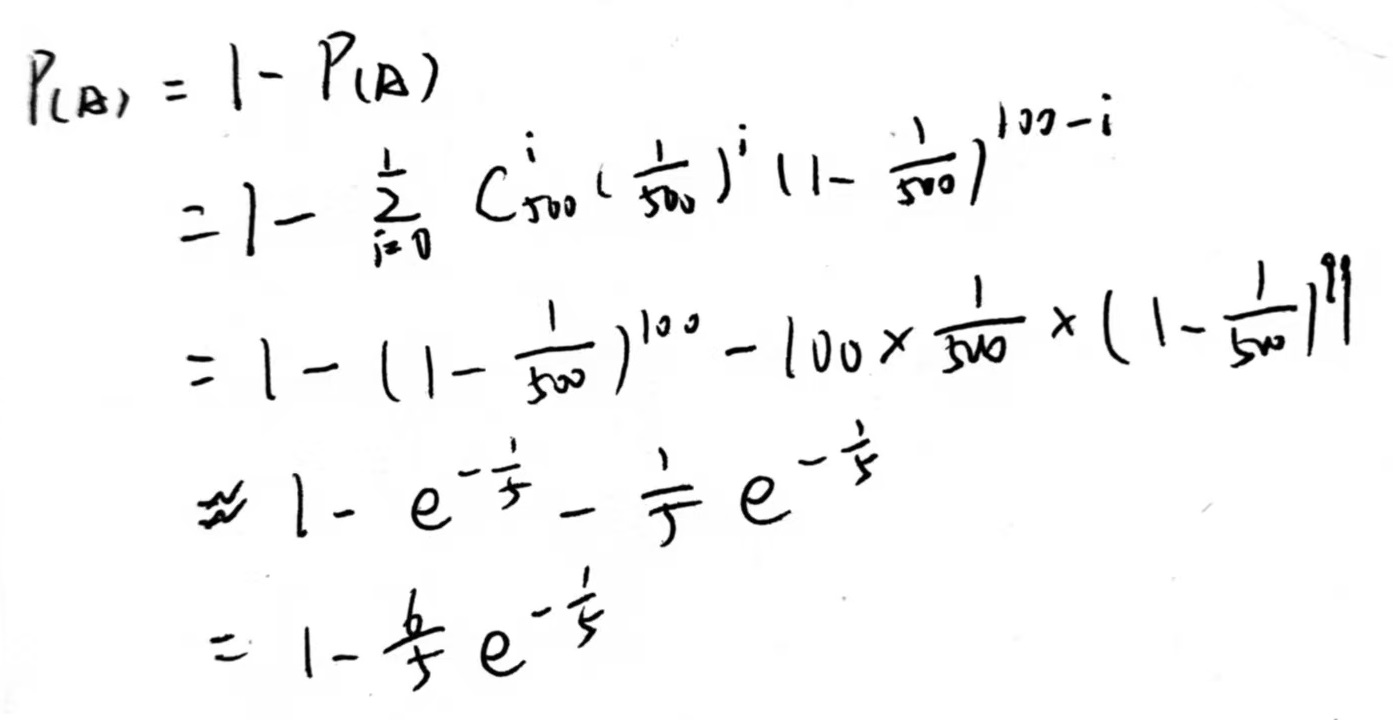
D

  • 连续型分布

    • 均匀分布 $X\sim U(a,b)$

    • 指数分布 $X\sim E(\lambda)$

      $t,s>0$时，$P{X\ge t+s|X\ge t}=P{X\ge s}$ 称为指数分布的无记忆性

      $EX=\frac1\lambda$称为平均寿命，也称为平均等待时间，$\lambda$称为失效频率，它是一个常数，失效频率不变，元件无损耗，才有无记忆性

    • 正态分布 $X\sim N(\mu,\sigma^2)$

      $\mu=0,\sigma=1$时为标准正态分布

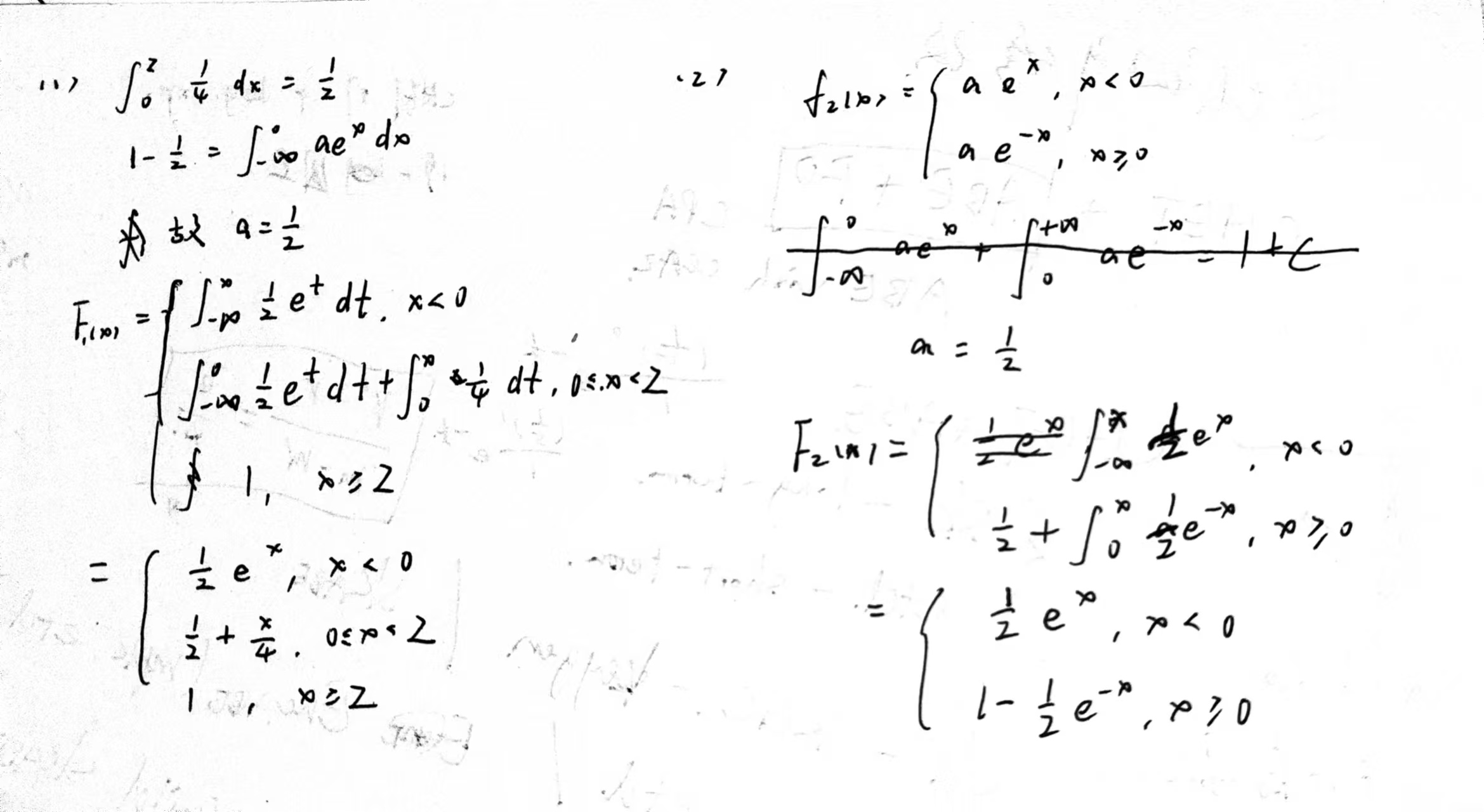
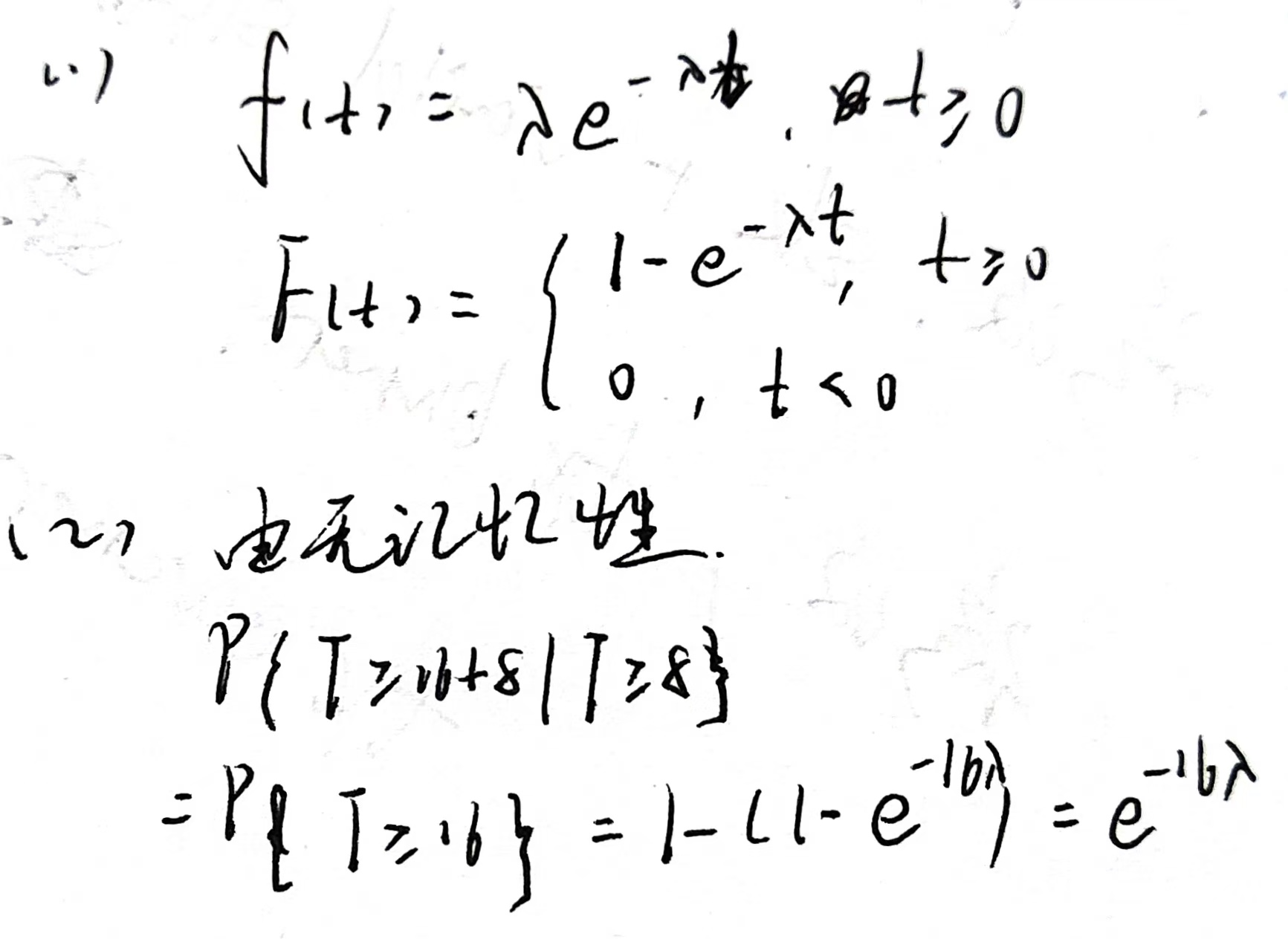
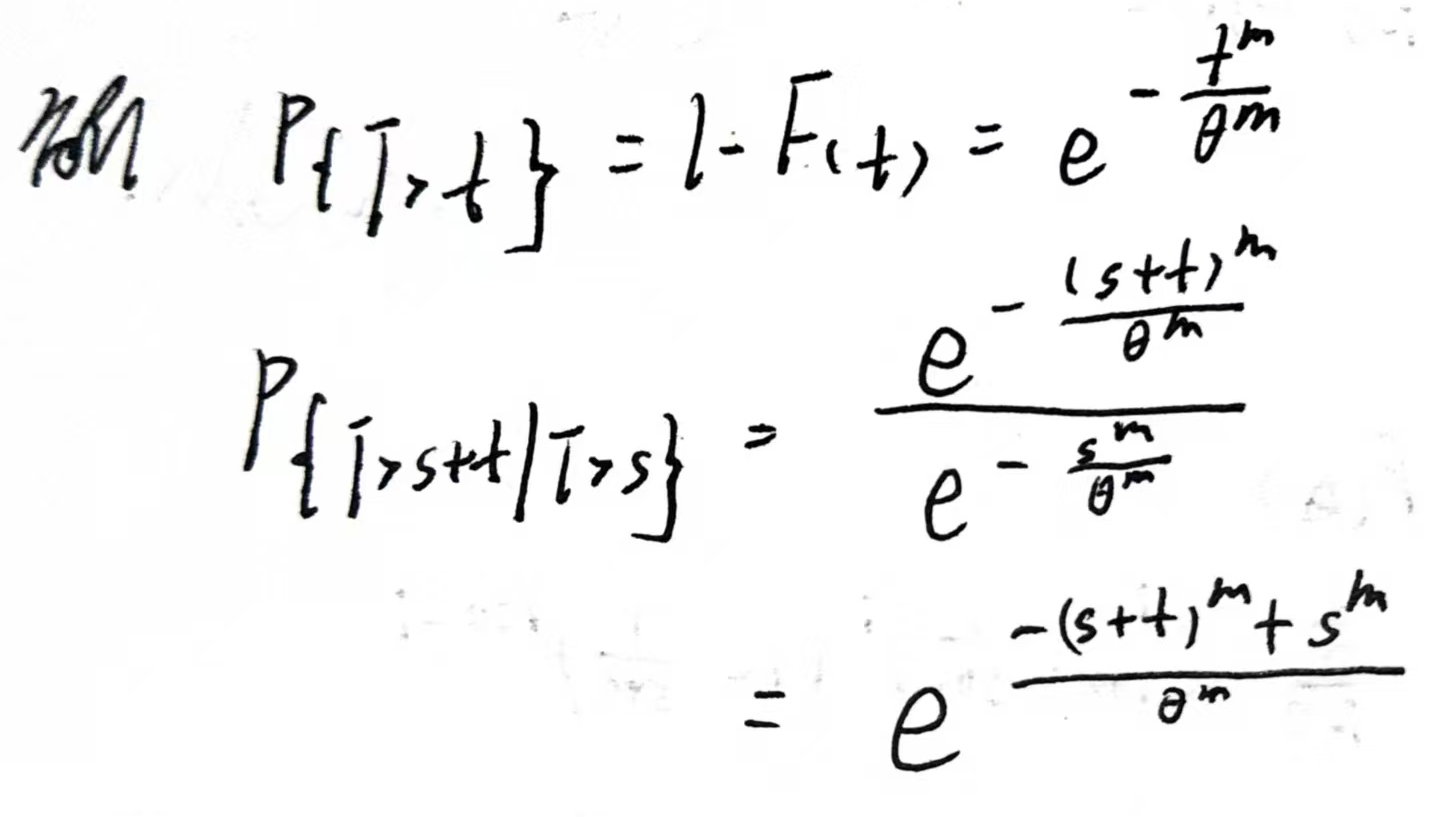
此分布为威布尔分布，是考虑元件损耗的寿命分布；若$m=1$，则成为指数分布，是理想元件（无损耗）的寿命分布

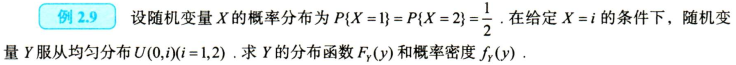
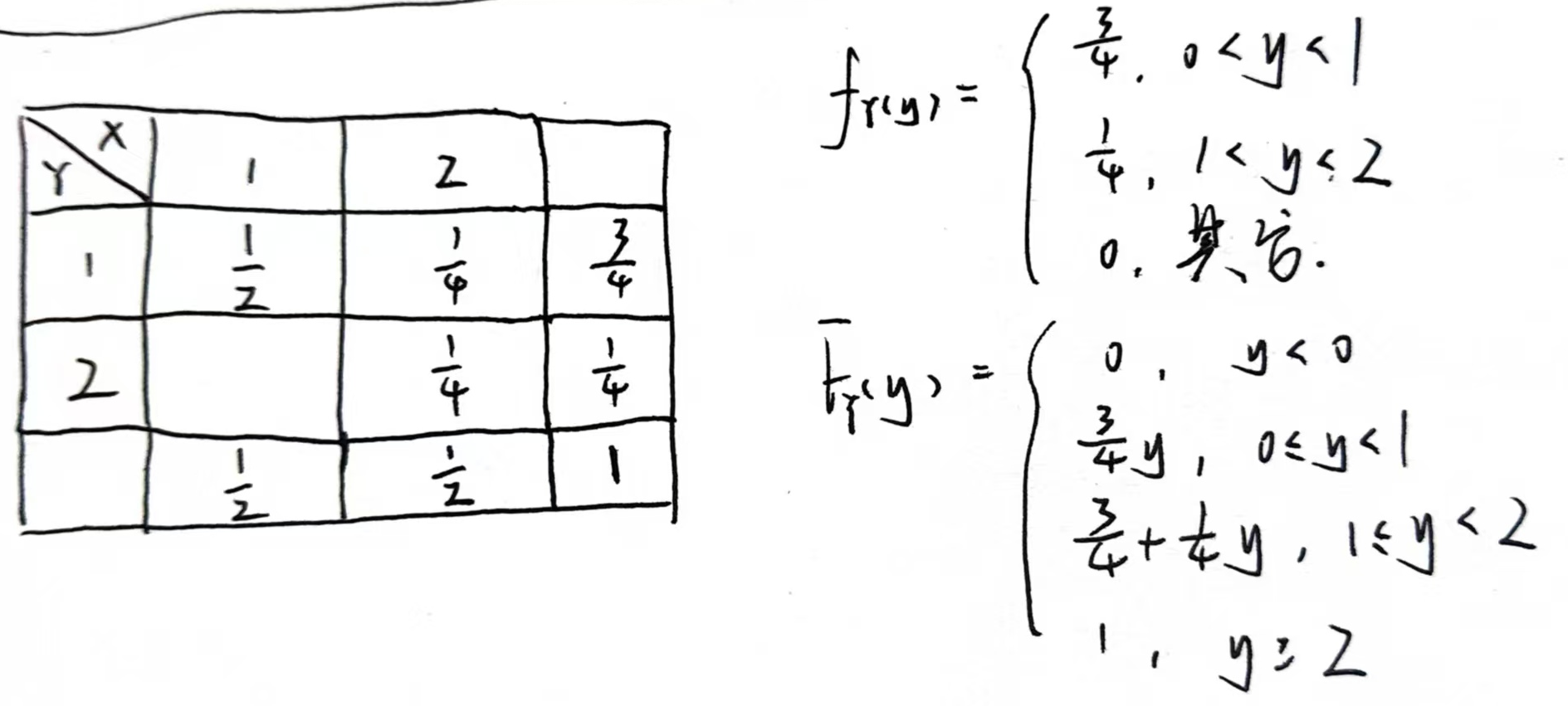
A

3.用分布

A

A

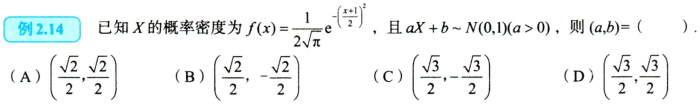
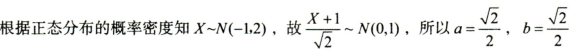
A

注意这里是$\ge$

$k\in[1,3]$

三、一维随机变量函数的分布

1.离散型->离散型

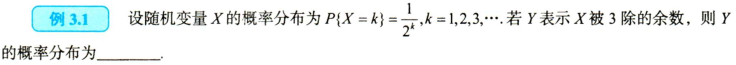
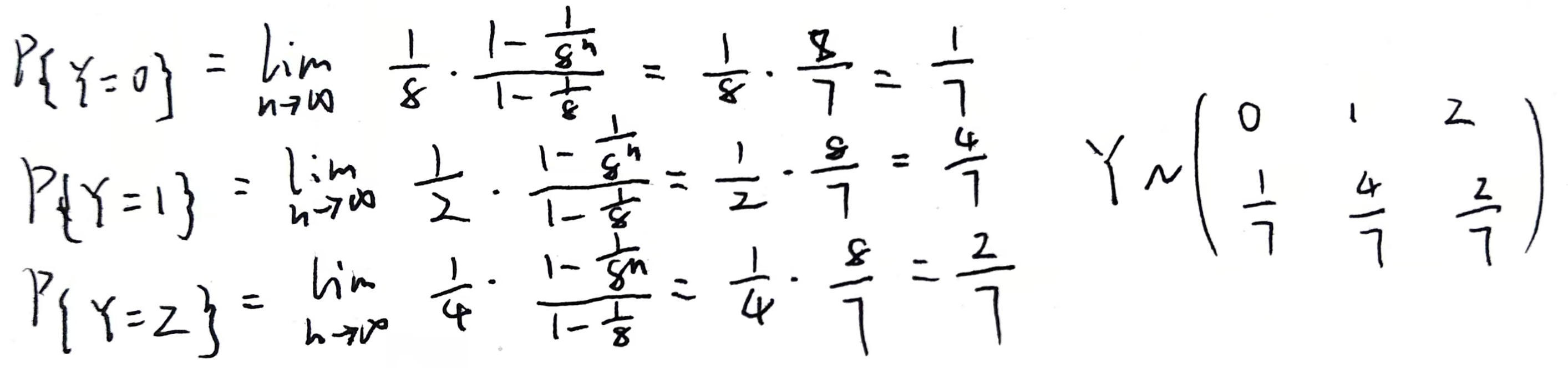
2.连续型->连续型（或混合型）

感觉讲解过程很复杂，还是直接看例题吧

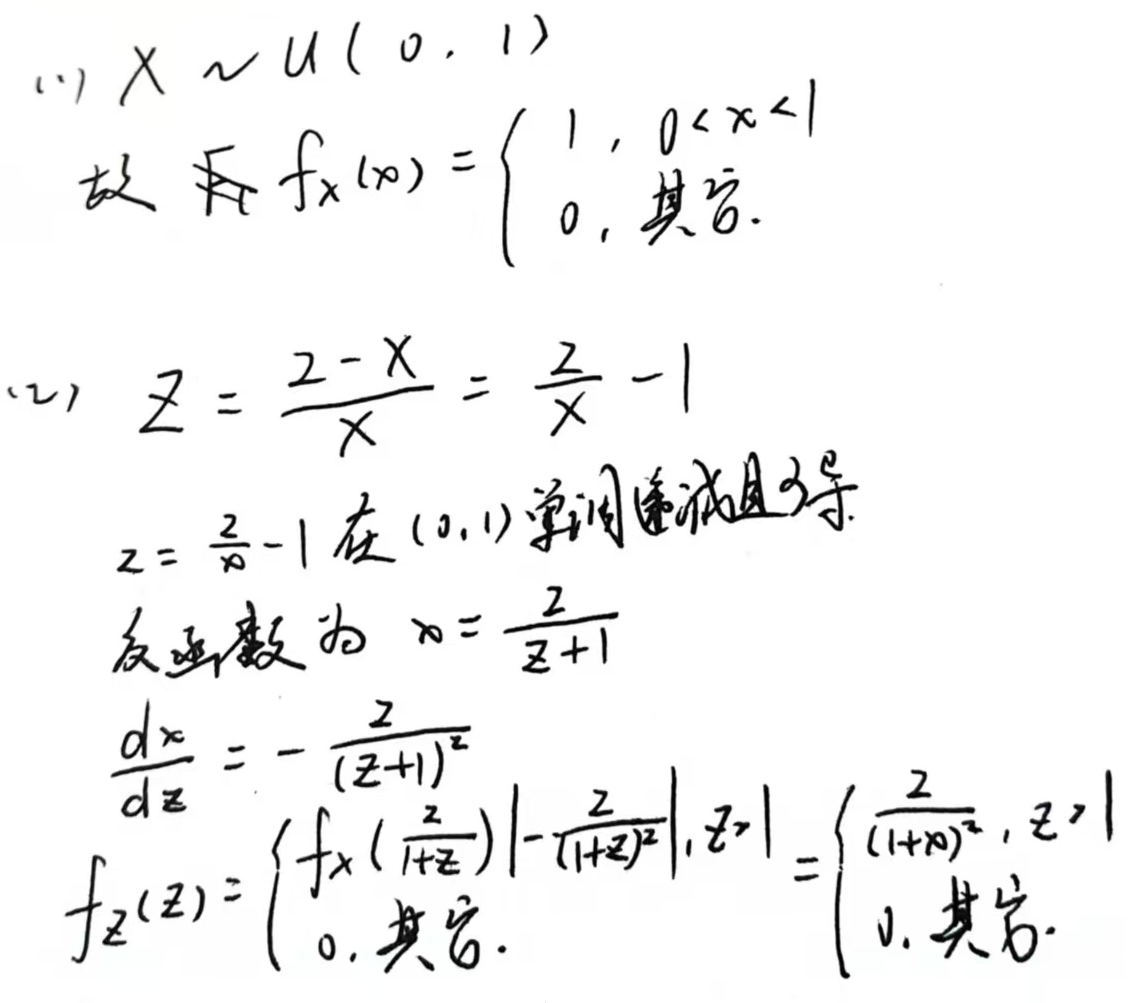
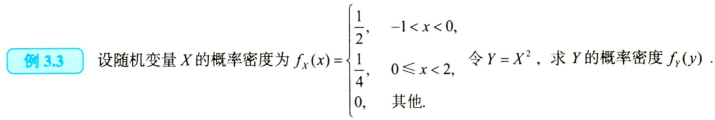
不是哥们，这玩意有点逆天

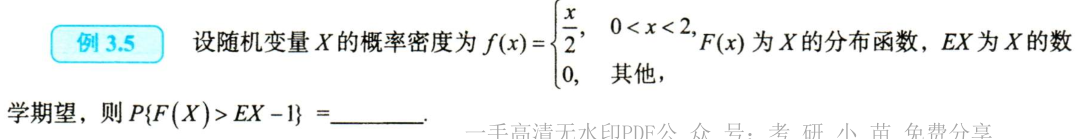
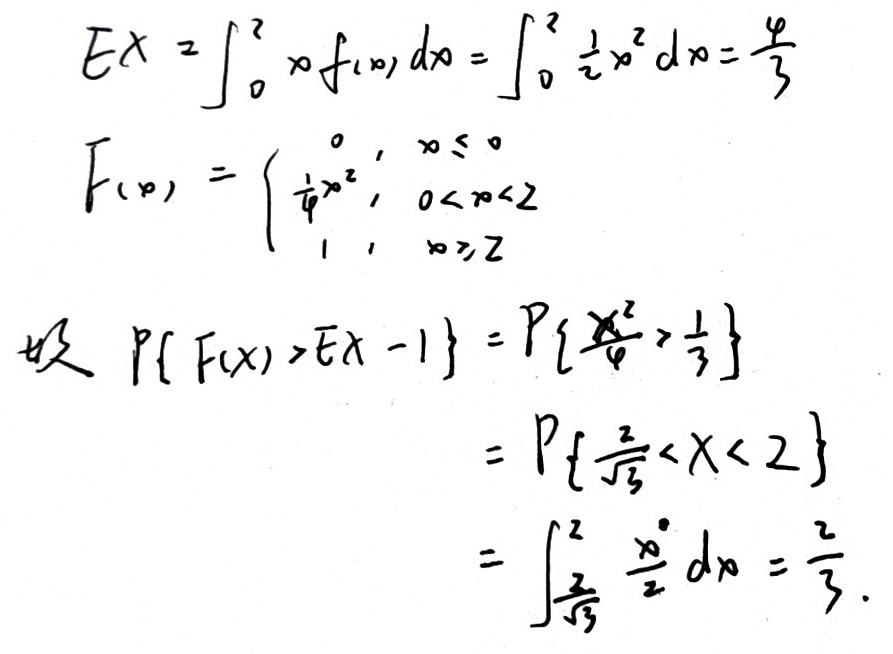
解法二有点不理解，但是好厉害···

3.连续型->离散型

若$X\sim f_X(x)$，且$Y= g(X)$是离散型随机变量；首先确定$Y$的可能取值$a$，然后通过计算概率$P{Y=a}$求得$Y$的概率分布

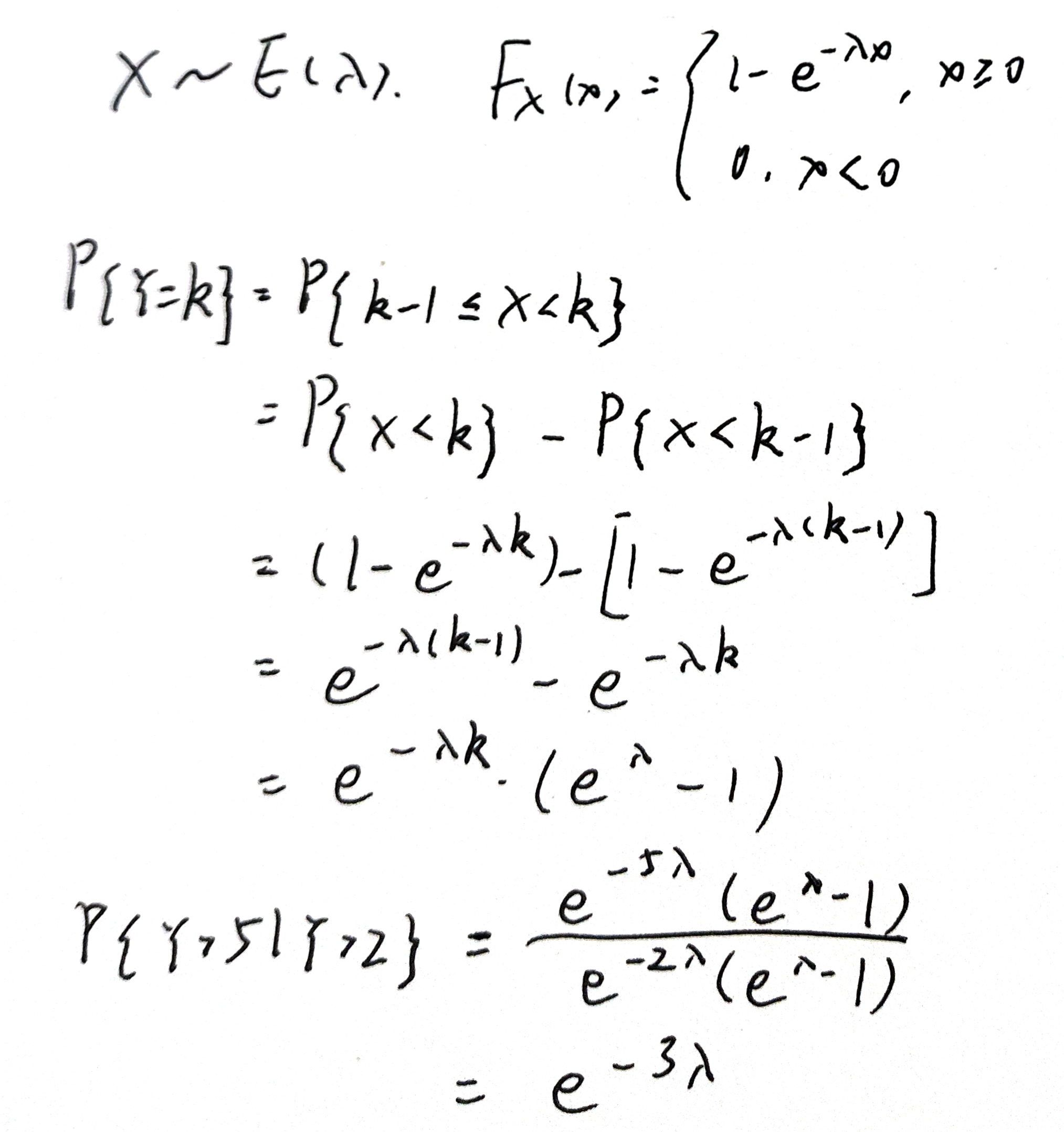
题解给的做法，直接用几何分布的无记忆性

四、多为随机变量及其分布

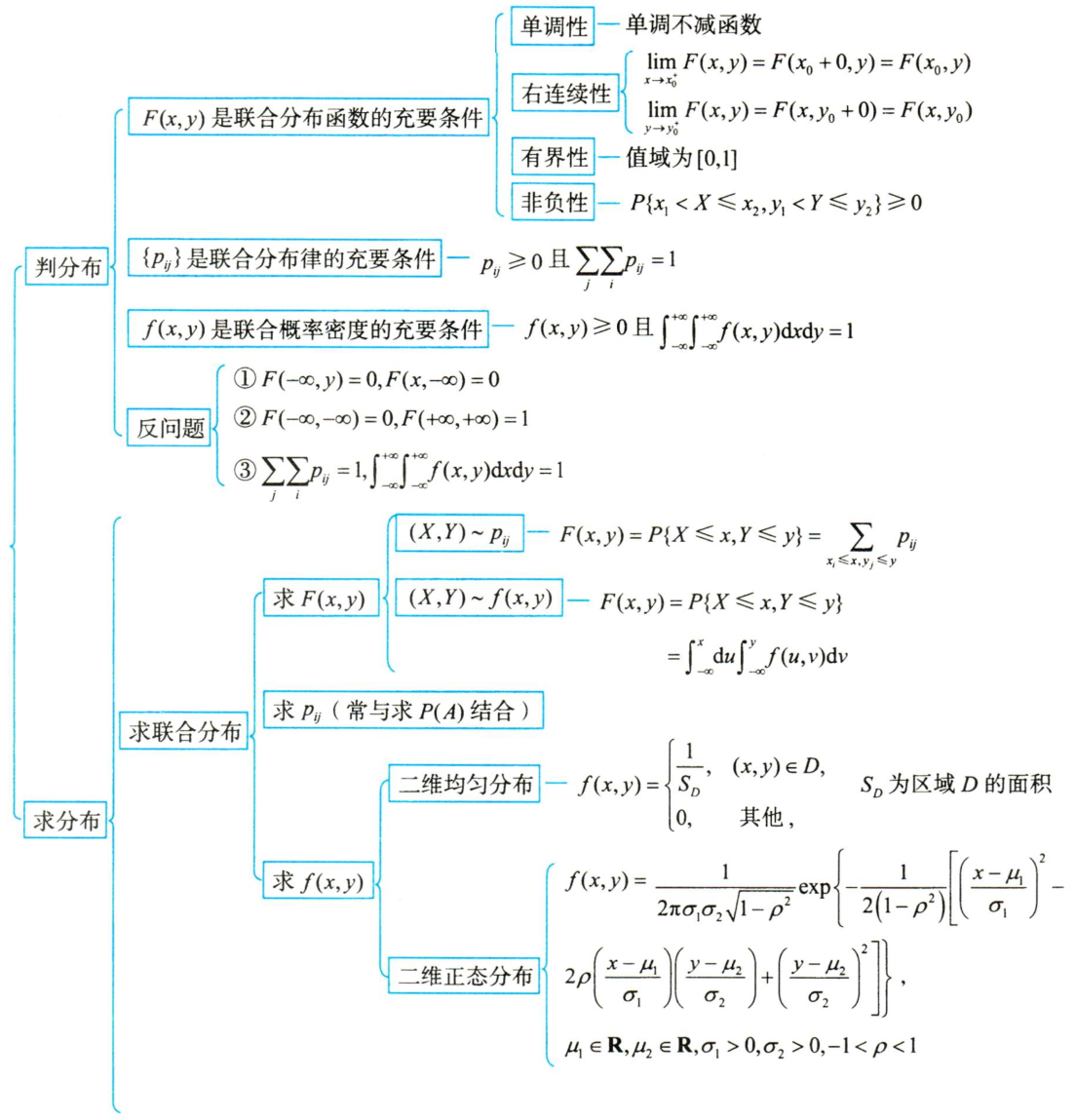
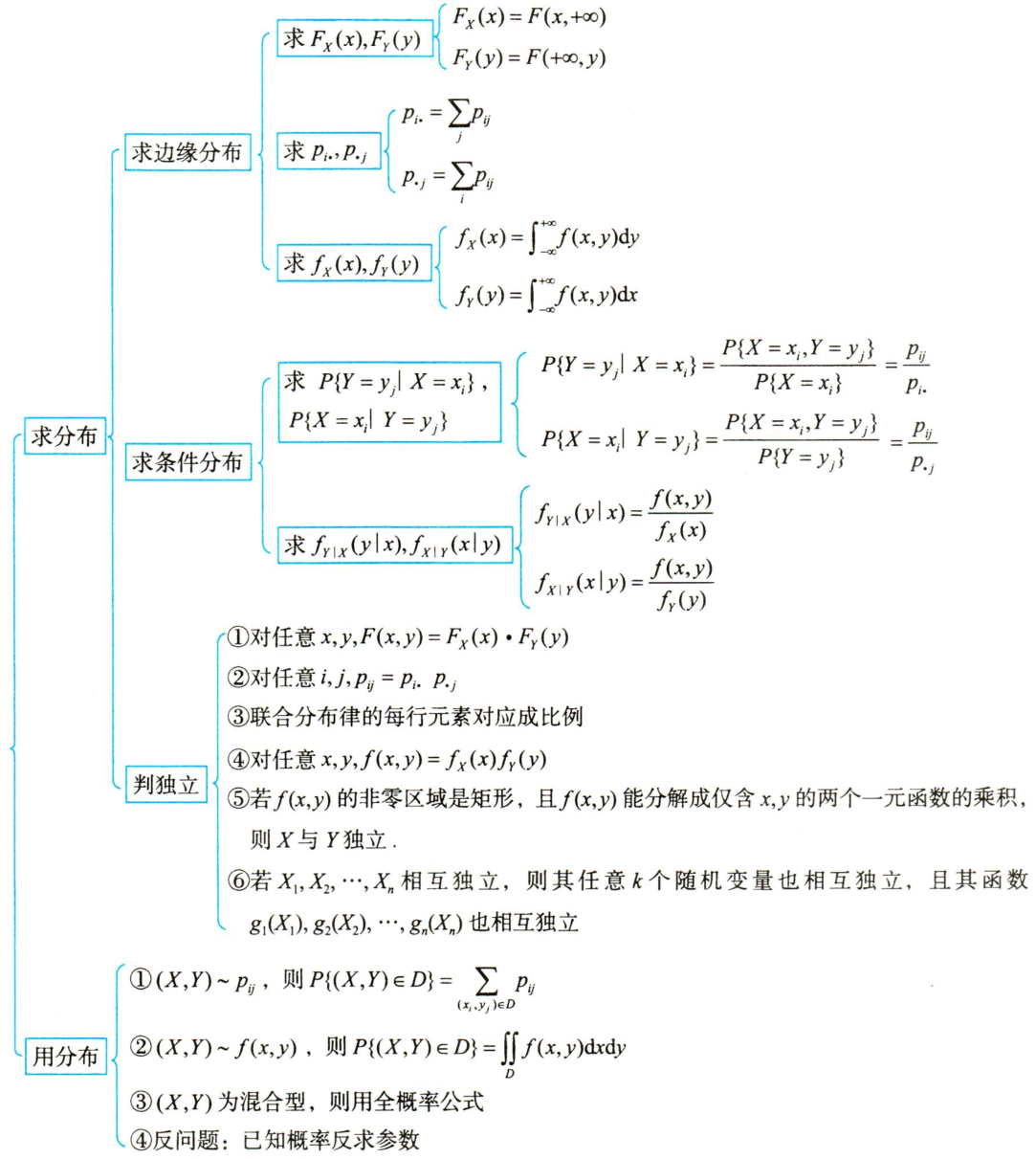
1.判分布

$F(x,y)$是联合分布函数的充要条件：单调性，右连续性，有界性，非负性

2.求分布

求联合分布

  • 求$F(x,y),p_{ij},f(x,y)$

    • $(X,Y)\sim p_{ij}$，则$F(x,y)=P{X\leq x,Y\leq y}=\sum_{x_i\leq x,y_i\leq y}p_{ij}$
    • $(X,Y)\sim f(x,y)$，则$F(x,y)=P{X\leq x,Y\leq y}=\int_{-\infty}^{+\infty}du\int_{-\infty}^{+\infty}f(u,v)dv$

  • 二维均匀分布

  • 二维正态分布 $(X,Y)\sim N(\mu_1,\mu2;\sigma_1^2,\sigma_2^2;\rho)$

求边缘分布

求条件分布

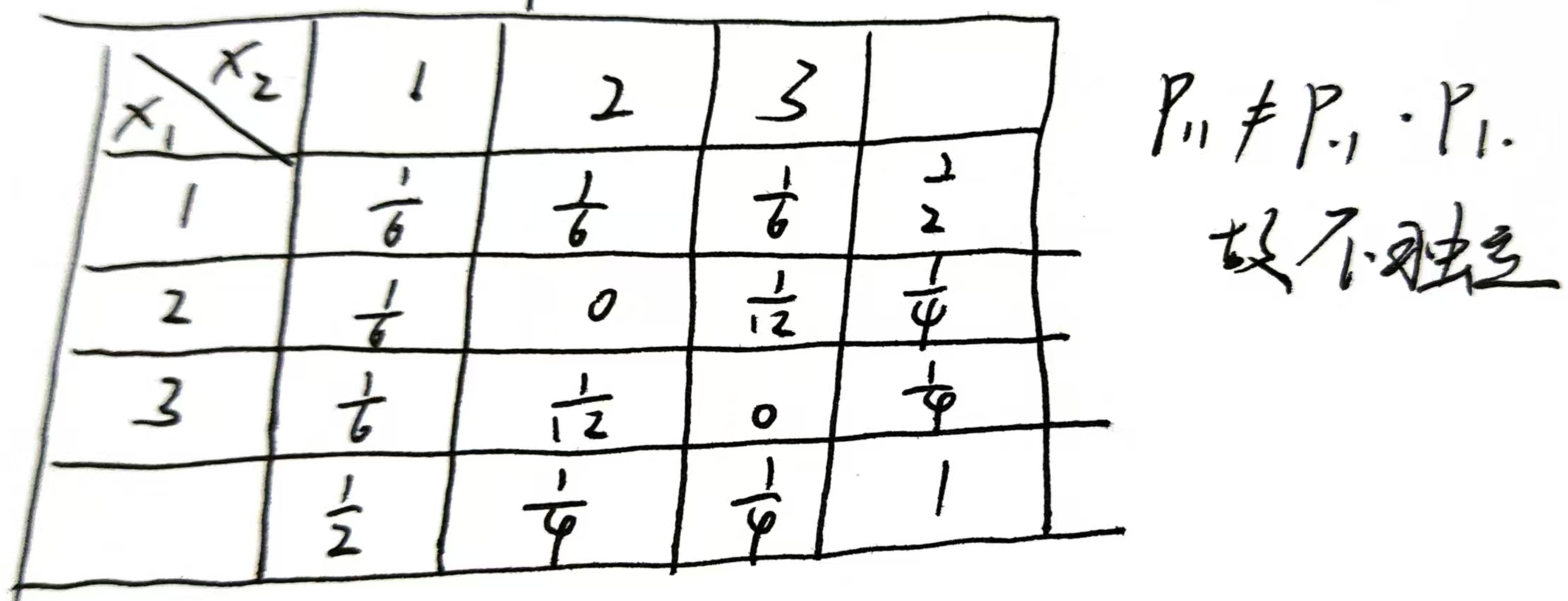
判独立

3.用分布

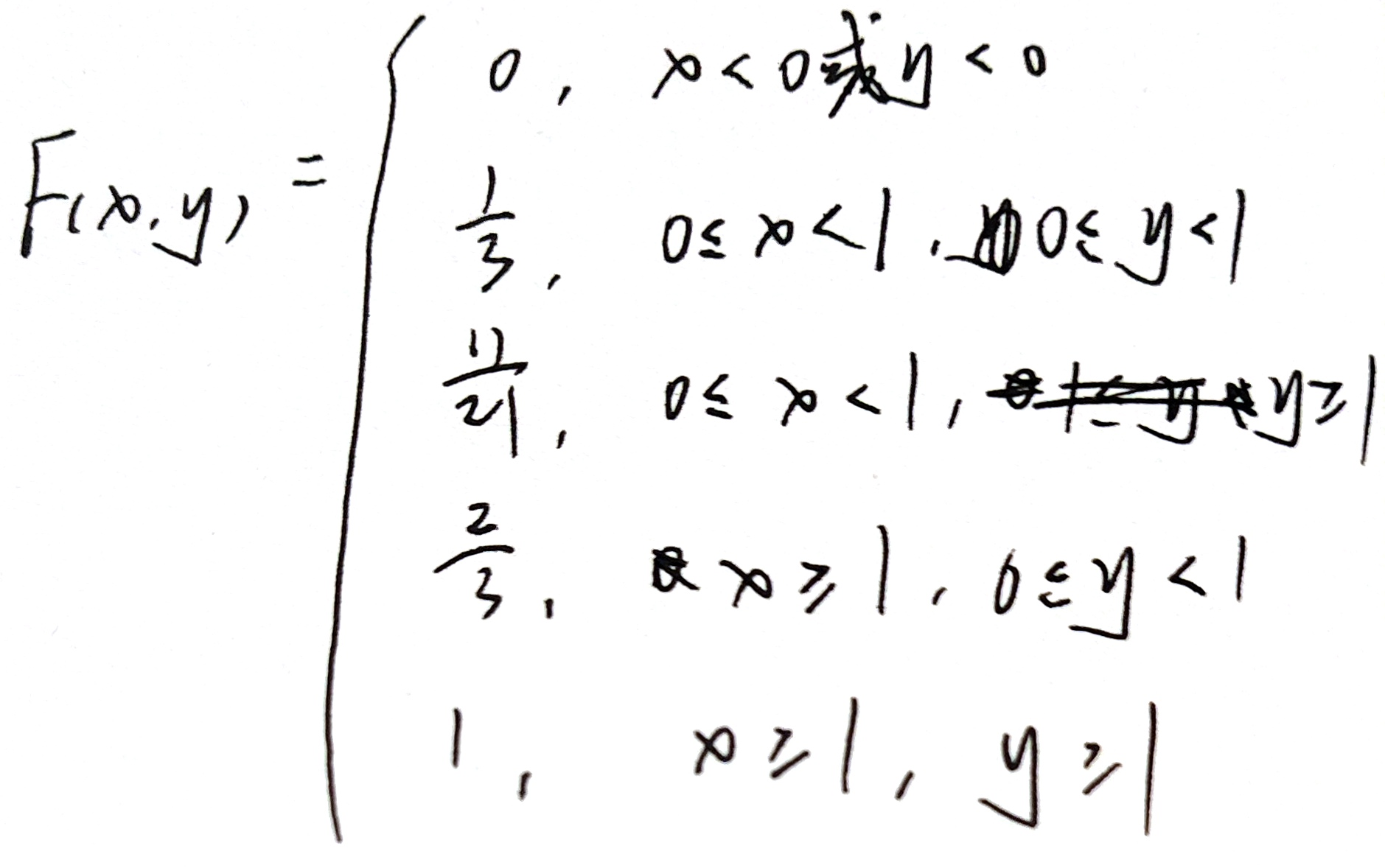
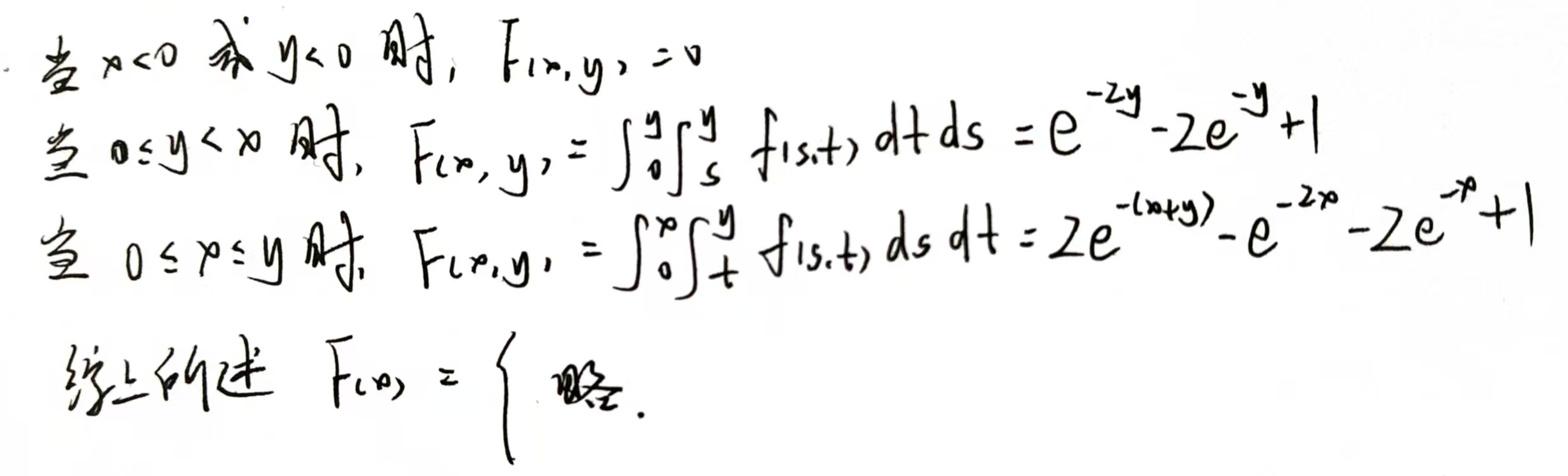
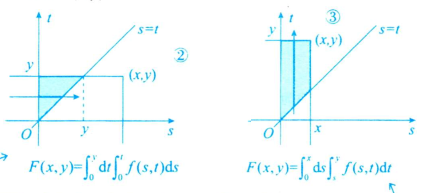
$a=0.1,b=0.1,c=0.5,d=0$

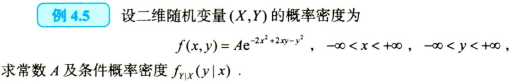
image-20241228211232751

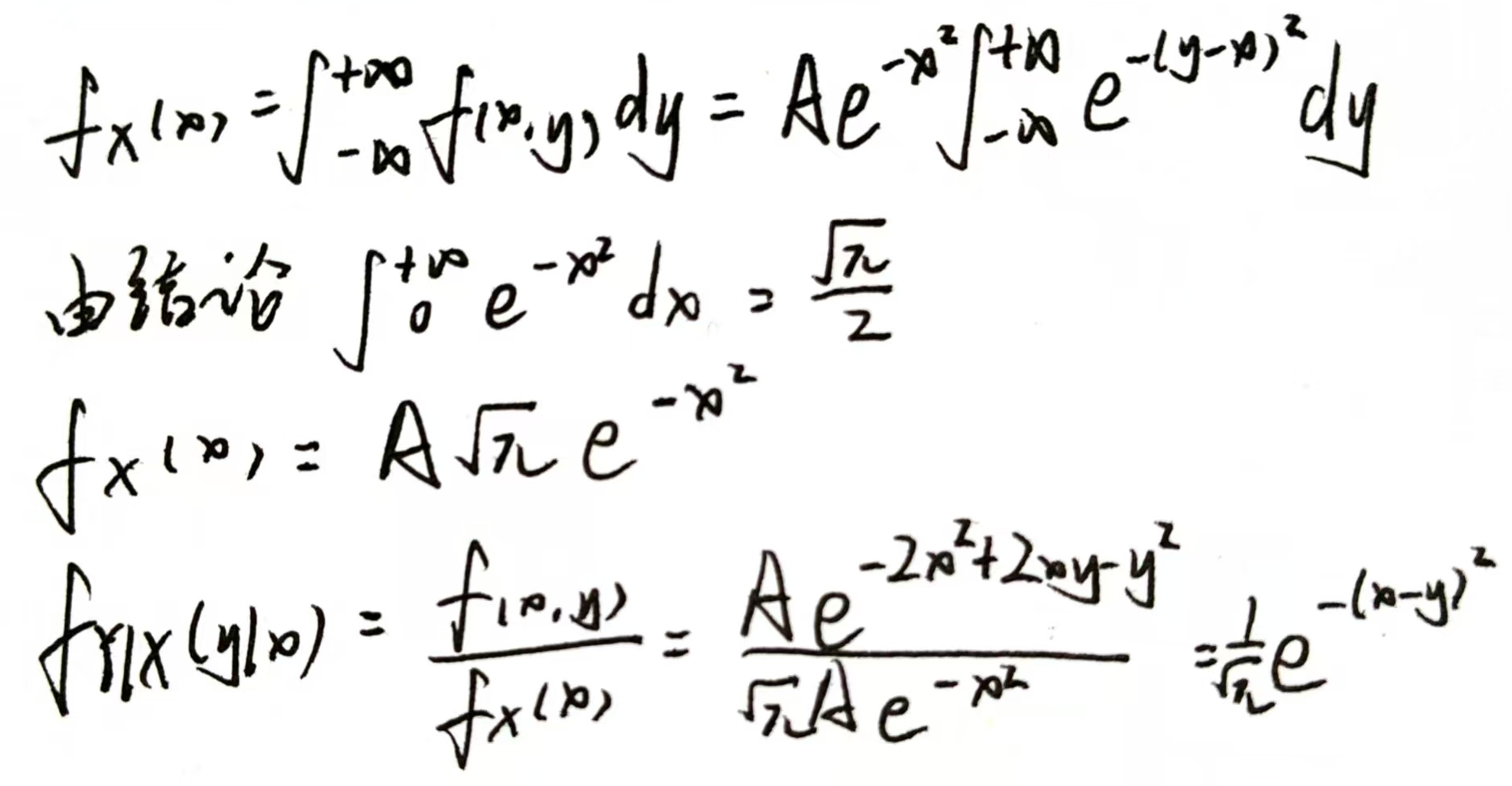
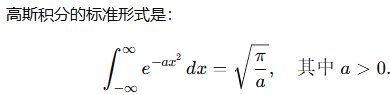
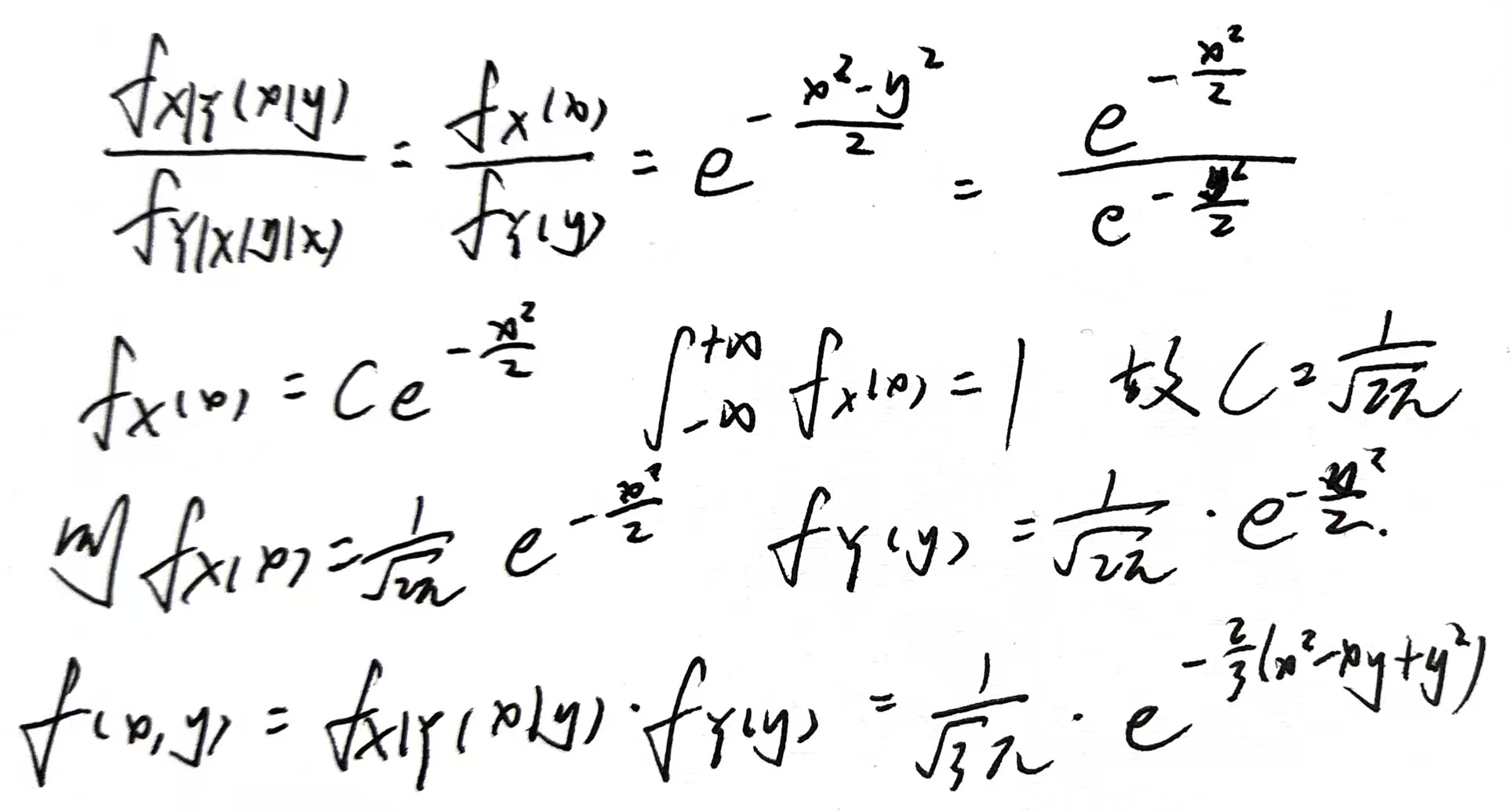
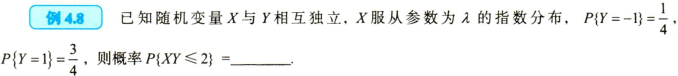
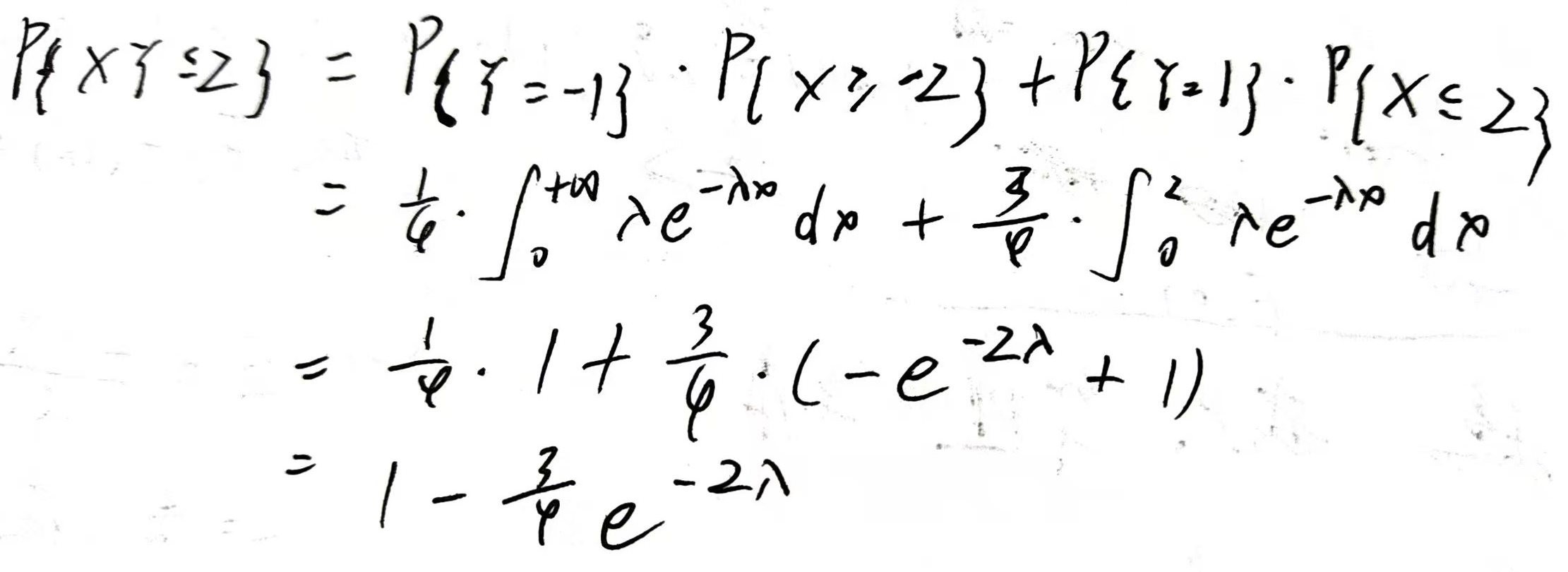
五、一维随机变量函数的分布

1.多维->一维

2.

3.

六、数学特征

1.数学期望

image-20241229151120087

2.方差

3.

七、大数定理和中心极限定理

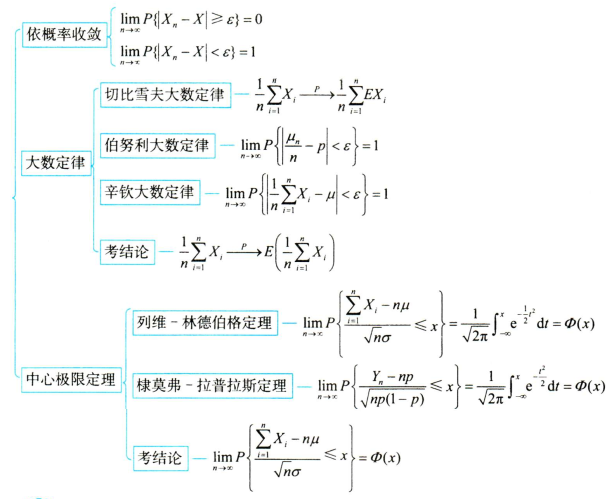
1.依概率收敛

设随机变量$X$与随机变量序列${X_n}(n=1,2,3,…)$，如果对任意的$\varepsilon>0$，有

则称随机变量序列${X_n}$依概率收敛于随机变量$X$，记为

$\lim_{n\to\infty}X_{n}=X(P)$ 或 $X_{n}{\overset{p}\longrightarrow}X(n\to\infty)$

2.大数定律

切比雪夫大数定律

相互独立 方差存在且一致有上界

则${X_n}$服从大数定理 $\frac1n\sum_{i=1}^nX_i\overset{p}\longrightarrow\frac1n\sum_{i=1}^nEX_i$

伯努利大数定律

$\mu_n$是$n$重伯努利实验中事件$A$发生的次数，$A\sim B(n,p)$，则 $\frac{\mu_n}n\overset{p}\longrightarrow p$

辛钦大数定律

相互独立 同分布 期望存在

则 $\frac1n\sum_{i=1}^nX_i\overset{p}\longrightarrow\mu$

大数定律同一个结论

$\frac1n\sum_{i=1}^nX_i\overset{p}\longrightarrow E(\frac1n\sum_{i=1}^nX_i)$

3.中心极限定理

列维-林德伯格定理

棣莫弗-拉普拉斯定理

中心极限定理同一个结论

八、统计量及其分布

1.统计量

样本均值 $\overline{X}=\frac1n\sum_{i=1}^{n}X_i$

样本方差 $s^{2}=\frac{1}{n-1}\sum _ {i=1}^ {n}(X_i-\overline{X})^{2} = \frac {1}{n-1}(\sum _ {i=1}^ {n}X_ {i}^ {2}-\overline{X}^2)$（无偏估计）

样本 $k$ 阶原点矩 $ A_ {k} = \frac {1}{n} \sum _ {i=1}^ {n} x^ {k} (k=1,2, \cdots )$

样本 $k$ 阶中心矩 $ B_ {k} = \frac {1}{n} \sum _ {i=1}^ {n} (X_ {i}-\overline {X})^ {k} (k=2,3, \cdots )$

顺序统计量 将样本n个观测量按其取值从小到大的顺序排列

2.统计量的分布

正态分布

略

$\chi^2$分布

3.正态总体下的常用结论

九、参数估计与假设检验

1.点估计和评价标准

2.区间估计与假设检验

Append

还有两个小时进考场，浅速通一下概率论

1
2
3
4
5
6
7
基本概率
联合概率求独立性
连续函数的概率密度
边缘密度和独立性
协方差
矩估计量和最大似然估计量
显著性水平应用题

协方差

$D(aX+bY)=a^2D(X)+b^2D(Y)+2abCov(X,Y)$

$Cov(X,Y)=E(XY)-E(X)E(Y)$

$\rho_{XY}=\frac{Cov(X,Y)}{\sqrt{D(X)}\cdot\sqrt{D(Y)}}$

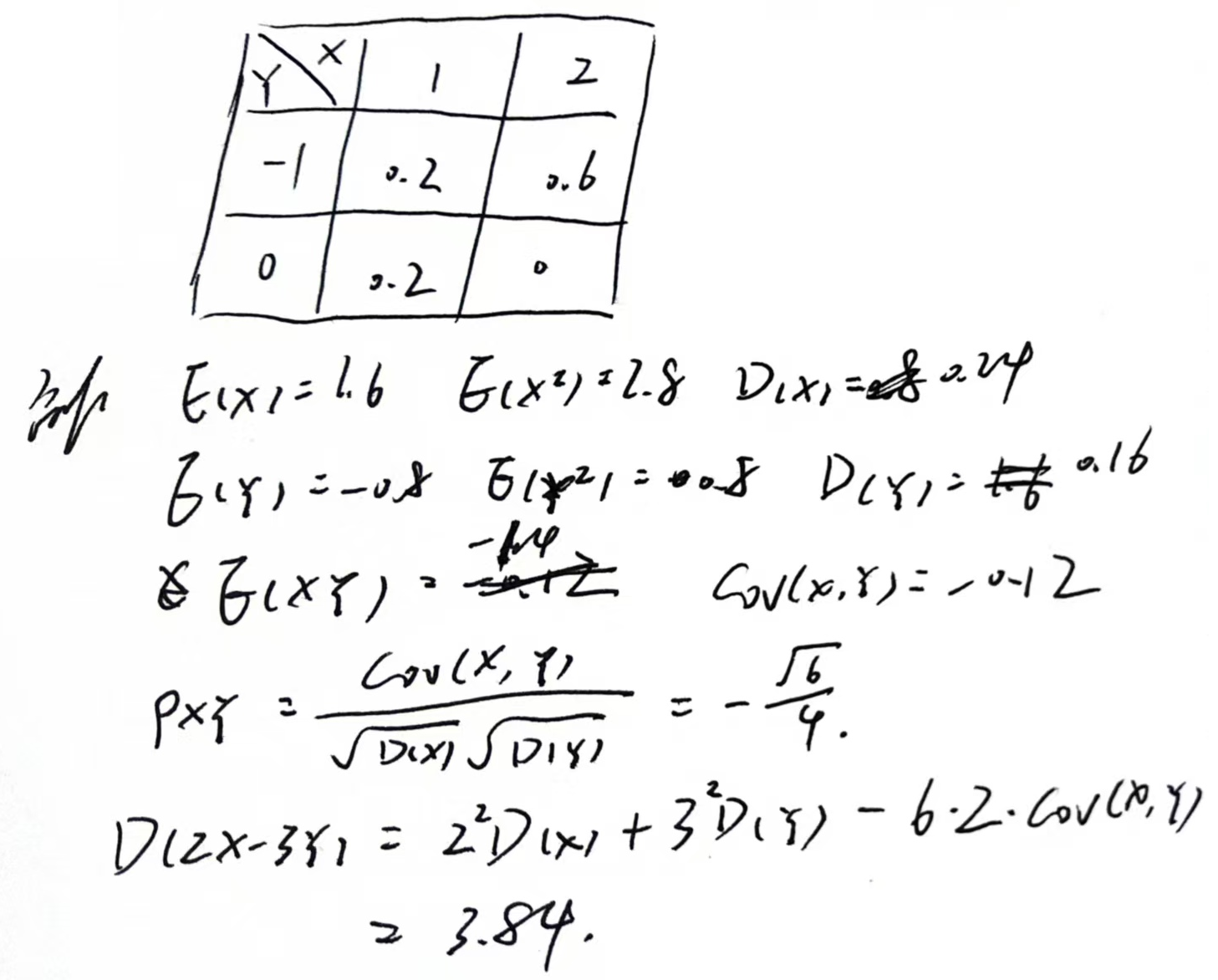
矩估计量和最大似然估计量

显著性水平应用题

要检验的假设是 $H_0: \mu$ 符合要求, $H_1:\mu$ 不符合要求（2分）